编辑推荐语
本书帮助读者入门深度学习深度学习入门，与其他深度学习入门图书的区别在于，本书中包含大量图解，并且采用口语化文字写作。由于作者是计算机图形学和深度学习方面的专家，所以在用图形图像来解释专业概念上具有一定优势和经验，因此本书中的大量图解也是本书一大特色。有了图解就意味着一些比较专业知识不一定需要用大量数学和公式去解释，所以这本书面向读者人群可以扩大到非计算机专业人士，哪怕是对深度学习、人工智能完全没有学习基础的人，也可以读懂。

作者简介

[美]安德鲁·格拉斯纳：

拥有北卡罗来纳州教堂山分校计算机科学博士学位，他是一位专门从事计算机图形学和深度学习的研究的科学家。他目前是Weta Digital（维塔数码）的高级研究科学家，致力于将深度学习与电影和电视世界级视觉效果的制作相结合。他曾在IBM沃森实验室、施乐PARC和微软研究所等实验室担任研究员。同时他也是最早的图形研究杂志ACM-TOG9(计算机图形学国际顶级期刊)的主编，和最早的计算机图形学会议SIGGRAPH（Special Interest Group for Computer GRAPHICS，由美国计算机协会计算机图形专业组组织的计算机图形学顶级年度会议）的技术论文主席。他撰写或编辑了十几本关于计算机图形学的技术书籍，包括著名的Principles of Digital Image Synthesis、Graphics Gems系列等。

译者简介：

赵鸣，2006年获华中师范大学计算机辅助教学硕士学位，2015年获哈尔滨工业大学计算机应用方向博士学位，现任长江大学教授。目前主持在研省部级项目四项，横向项目两项。他的研究兴趣包括计算智能、图像和信号处理、模式识别等。他是荆州市智慧警务专家成员，也是IEEE高级成员

 曾小健，出版AI图书多部，在量化金融和AI领域有多年经验，计算机博士在读，CSDN博客专家，多个大模型开源项目源码贡献人，曾在华为云、中关村在线等多所大型互联网科技企业担任重要职务，GitHub：ArtificialZeng; CSDN:AI生成曾小健。

 李现伟，日本早稻田大学博士毕业，硕士生导师，主要从事大数据、机器学习、物联网等方向的教学与工作。发表SCI论文20余篇，主持和参与安徽省自然科学基金、安徽省重点研究与开发计划、安徽省教育厅优秀青年基金项目等多项。获得中国发明协会创业奖成果奖二等奖，获得绿色矿山科学技术奖二等奖一项。

任玉柱，毕业于国防科学技术大学网络工程专业，主要研究方向为信息安全，机器学习，人工智能，发表相关领域研究文章3篇。

内容简介

本书适合任何想要深入了解深度学习这个迷人领域的人，您不需要具备高级数学和编程知识就可以掌握其根本原理。如果您想知道这些工具是如何工作的，并学会自己使用它们，答案尽在书中。而且，如果您已经准备好编写自己的程序，那么随附的Github存储库中还有大量补充的Python笔记本可以帮助您。

本书讲解语言通俗易懂，包含大量的的彩色插图和具有启发性的类比，以及丰富的现实世界的例子，深入地地解释了深度学习的关键概念，包括:

•文本生成器如何创建新颖的故事和文章。

•深度学习系统如何在人类游戏中学习游戏并获胜。

•图像分类系统如何识别照片中的物体或人。

•如何以对日常生活有用的方式思考概率。

•如何使用构成现代人工智能核心的机器学习技术。

各种各样的智力冒险家都可以使用本书中涵盖的强大思想来构建智能系统，帮助我们更好地理解世界和生活在其中的每个人。这就是人工智能的未来，这本书可以让你充分想象它的未来。

精彩文摘（纯文字）

第15章 优化器

训练神经网络通常是一个非常耗时的过程，任何能加速这个过程的方法都将受到我们的欢迎。本章将介绍一系列优化神经网络的方法，这些方法旨在通过提高梯度下降的效率来加快学习速

度。我们的目标是使梯度下降运行得更快，并避免一些可能导致其陷入困境的问题。这些方法还自动完成了一些寻找最佳学习率的工作，包括可以随着时间的推移自动调整学习率的算法。这些方法统称为优化器。每个优化器都有其优点和缺点，为了在训练神经网络时做出正确的选择，我们需要了解它们。让我们先绘制一些能够直观地表示误差的图形，并观察误差是如何变化的。这些图形将帮助我们建立一些与后面介绍的算法相关的基础知识。

15.1　用二维曲线表示误差

从几何思想的角度来思考系统中的错误是比较直观的，所以我们经常将误差绘制为二维曲线。

为了熟悉这种二维误差曲线，我们参考一个将两个类的样本拆分为排列在一条线上的点的示例。负值处的点属于一类，零及正值方向的点属于另一类，如图15-1所示。图15-1：一条线上的两类点。0值左边的点为类0，用蓝色表示；其他点为类1，用黄色表示让我们为这些样本构建一个分类器。在本例中，边界仅包含一个数字。该数字左侧的所有样本都分配给类0，右侧的所有样本则分配给类1。想象如果我们沿着这条线移动这个分界点，就可以计算出被错误分类的样本数量，并称之为误差。我们可以将结果总结为一张图，其中X轴显示了每个潜在的分界点，与该点相关的误差绘制为其上方曲线中的一个点。图15-2显示了这个过程。

根据第14章介绍的使用平滑误差函数曲线计算梯度（从而应用反向传播算法）的方法，我们可以对图15-2的误差曲线进行平滑处理，如下页图15-3所示。

对于这组特定的随机数据，边界点为0或者0左边一点时，误差是0。因此不管从哪

里开始，我们都希望分类器最终在0这一点结束。

我们的目标是找到一种方法来定位任何误差曲线的最小值。如果能做到，就可以将

其应用于神经网络的所有权重，从而减少整个神经网络的误差。

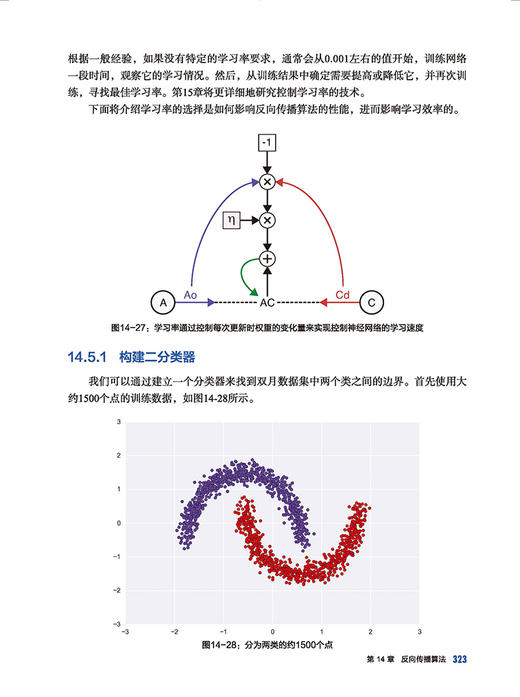
15.2　调整学习率

使用梯度下降来训练系统时，最关键的超参数是学习率，通常用小写希腊字母

η(eta)表示，取值范围在0.01至0.0001之间。η取较大的值会带来更快的学习，但可能

会导致我们过度调整神经元的参数，从而错过误差的最佳取值（波谷）。η取较小的值

（ 接近0，但始终为正）会导致学习速度减慢，并可能陷入局部的波谷（局部最优解），

即使附近有更深的波谷（全局最优解），它们也可能永远无法到达。下页图15-4以图形

方式概括了这些现象。

许多优化器都包含一个重要思想，那就是我们可以通过改变学习率来提高学习效

率。这种思想类似于使用金属探测器在海滩上寻找埋藏的金属。我们首先要迈出大步，

在海滩上寻找大致的位置，但当探测器亮起，我们会采取越来越小的移动步伐来确定金

属物体的详细位置。同样，我们通常在深度学习过程的早期沿着误差曲线迈出大步，同

时寻找低谷。随着时间的推移，越来越接近它的最低点，采取的学习率也越来越小，最

终找到那个山谷。

我们可以用一条简单的误差曲线来表示这个优化器，该曲线包含一个孤立的具有负

高斯曲线形状的谷值，如图15-5所示。

为了清晰展示，图15-6中的坡度已缩小到其实际值的25%。我们可以看到，该曲线

小于0的输入值，梯度为负；而大于0的输入数值，梯度为正。当输入为0时，处于碗的

最底部，因此那里的梯度为0，仅绘制为一个点。

15.2.1　恒定大小的更新

首先来观察使用恒定的学习率时会发生什么？换句话说，总是用相同的η值来缩放梯度，该值在整个训练过程中保持不变。图15-7显示了恒定大小更新的基本步骤。