《更加了解虛數：平方為負的神奇數》

作者：日本Newton Press

譯者：衛宮紘

出版社：人人出版

出版日期：2021/05/05

語言：繁體中文

ISBN：9789864612390

叢書系列：人人伽利略科學叢書

規格：平裝 / 176頁 / 21 x 27.5 x 0.8 cm / 普通級 / 全彩印刷 / 初版

出版地：中國台灣

本書分類：自然科普> 數學> 概論

（页面参数仅供参考，具体以实物为准）

內容簡介

★日本牛頓獨家授權精美圖解

★符合一○八課綱學習素養，延伸學習觸角

★學習虛數與複數的重要概念

「什麼是虛數？」這個問題如果答不太出來的話，那麼，「少年伽利略」的《虛數》或許可以幫助你釐清觀念。

虛數是從imaginary number翻譯而來，之所以是「想像」的，是因為它並不實際存在。虛數用i來代表，其定義是(-1)的平方根。從剛開始的整數，進而發現分數、小數、根號，好不容易接受了0跟負數的概念，卻又出現了平方之後竟然是負的，這跟一般「負負得正」的概念是相反的。虛數到底有什麼用處呢？

──有了將虛數與實數加起來的「複數」，想要用數學式表現波動、聲音、電磁波，便可化繁為簡。

──想要了解量子力學的基礎方程式，一定要學好虛數。

──利用傅立葉轉換的降噪耳機，也用了以虛數為主角的歐拉公式。

──與相對論有關的四維距離，流動著虛數時間？

虛數看似與生活無關，其實很重要。理解虛數，不要求快，踏實最重要，《虛數》以精彩圖片搭配解說，從數的發展脈絡開始講解，帶領讀者一起釐清虛數和複數的基礎概念及其運用。

系列特色

1. 本書系取得日本牛頓出版社的授權，以精美插圖、珍貴照片及電腦模擬圖像，深入淺出解說科學知識，淺顯易懂。

2. 以一書一主題的系統化，縱向深入閱讀，橫向觸類旁通，主題涵蓋天文、數學、物理、化學、生命科學等領域。

3. 以不同的角度提出各種科學疑問，啟發讀者對科學的探究興趣。

目錄

一、虛數的誕生歷程

自然數

零

負數

負數的乘法

有理數 ①∼②

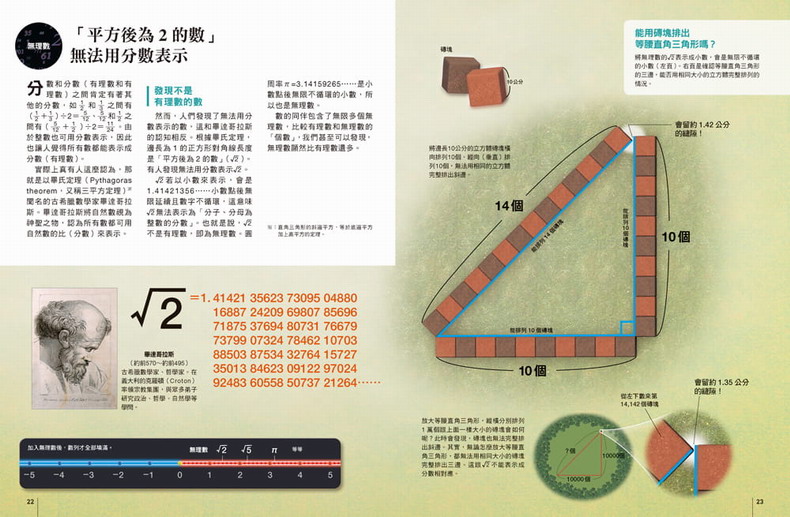
無理數

實數

Column 1 小數的表示法誕生於16世紀

Column 2 畢達哥拉斯認為有理數是數的一切

Column 3 古代美索不達米亞黏土版刻畫的 2

Column 4 古人是這樣作平方根的圖

Column 5 證明 2是無理數

Column 6 用分數表示 2的方法—連分數

Column 7 何謂方程式？

Topics 實數的完成與無窮的概念

二、何謂虛數

虛數是什麼？

解不開的問題

虛數的誕生 ①∼②

虛數獲得市民權

Column 8 「二次方程式」不一定有實數解

Column 9 有4000年歷史的「二次方程式」

Column 10 以二次方程式的「公式解」求解卡當諾問題

Column 11 虛數誕生的契機是16世紀的 「數學擂台」

Column 12 卡當諾喜歡賭博，還促成 機率論發展

Q&A 1 複數平面為何又稱「高斯平面」？

Q&A 2 虛數能比較大小嗎？

三、虛數與複數

複數的表示方式

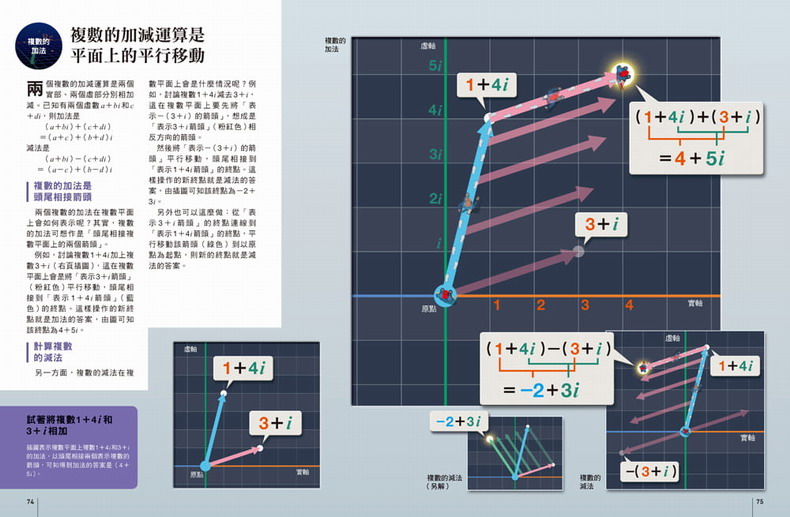
複數的加法

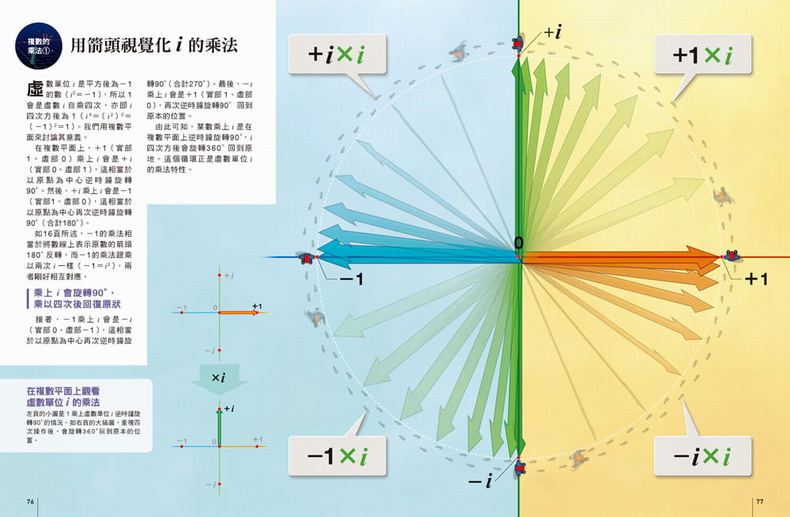
複數的乘法 ①∼②

以虛數求解奇妙的謎題 ①∼②

高斯與複數 ①∼②

數擴張的終點站

Column 13 以複數平面確認

「卡當諾問題」

Column 14 為什麼不是「負負得負」？

Column 15 複數的「極式」是什麼？

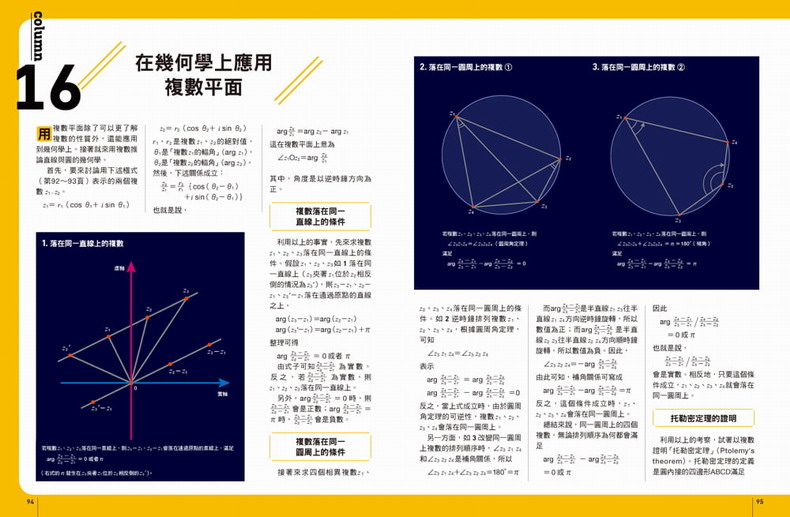
Column 16 在幾何學上運用複數平面

Column 17 複數平面的反轉與無窮遠點

Q&A 3 －1的四次方根、八次方根、十六次方根該如何計算？

Column 18 證明「代數基本定理」

Column 19 碎形與複數

Column 20 以複數的牛頓法求解碎形

Topics 黃金比例、正五邊形與複數

四、人類的至寶歐拉公式

三角函數

泰勒展開 ①∼②

何謂虛數次方？

歐拉的兩個公式

π、i與e

鑑賞歐拉公式

為什麼歐拉公式重要？

Column 21 何謂三角函數？

Column 22 何謂自然對數的底數「e」？

Column 23 何謂圓周率「π」？

Column 24 為近代數學奠基的天才

數學家歐拉

五、虛數與物理學

光、天體與虛數

四維時空與虛數 ①∼②

未知粒子與虛數

量子力學與虛數 ①∼③

Q&A 4 為什麼不存在的虛數跟自然界有關？

Topics 量子力學與複數

Topics 小林－益川理論與虛數