书名：斯特朗线性代数  
定价：119.8  
ISBN：9787115676849  
作者：[美] 吉尔伯特·斯特朗（Gilbert Strang）  
版次：第1版  
出版时间：2025-10  

内容提要：  
本书直观地讲解了线性代数这门学科，通过简单的线性方程组引出矩阵的基本概念和运算，详细介绍了向量空间、线性变换、正交性、行列式、特征值与特征向量等理论知识，以及其在统计学、计算机科学、物理学、工程学、经济学等领域中的应用，特别是线性规划、网络模型、博弈论等内容。语言通俗易懂，示例丰富。每章*有大量习题，并给出了部分习题的解答。另附附录、词汇表及MATLAB 教学代码等，为课程教学和自学提供了*支持。  



作者简介：  
吉尔伯特·斯特朗（Gilbert Strang），美国数学家，美国国家科学院院士，麻省理工学院数学系退休教授。他在有限元理论、变分法、小波分析和线性代数等领域均有*的成*。曾担任美国国家数学委员会主席、美国工业与应用数学学会主席。 作为全球高等数学教育界的传奇人物，他出版了包括本书在内的13部广受好评的教科书和专著，其开设的多门公开课程在互联网上的累计浏览量已达数千万次。  

目录：  
第 1章 矩阵与高斯消元法 1  
1.1 引言 1  
1.2 线性方程组的几何意义 4  
1.2.1 列向量和线性组合 6  
1.2.2 奇异情形 8  
习题 10  
1.3 高斯消元法的一个例子 12  
1.3.1 失效的消元法 14  
1.3.2 消元运算的成本 15  
习题 16  
1.4 矩阵定义与矩阵乘法 20  
1.4.1 矩阵与向量的乘法 21  
1.4.2 消元步骤的矩阵形式 23  
1.4.3 矩阵乘法 24  
习题 28  
1.5 三角因子和行交换 33  
1.5.1 A=LU：n×n的情形 36  
1.5.2 一个线性系统=两个三角形系统 37  
1.5.3 行交换与置换矩阵 39  
1.5.4 简易消元法：PA=LU 41  
习题42  
1.6 矩阵的逆和转置 47  
1.6.1 A^{ 1}的计算方法：高斯–若尔当法 49  
1.6.2 可逆=非奇异（n个主元） 51  
1.6.3 转置矩阵 52  
1.6.4 对称矩阵 53  
1.6.5 对称矩阵RTR、RRT和LDLT 53  
习题 54  
1.7 特殊矩阵及其应用 61  
习题 66  
第 1章复习题 67  
第 2章 向量空间 71  
2.1 向量空间和子空间 71  
2.1.1 矩阵A的列空间 73  
2.1.2 矩阵A的*空间 75  
习题 76  
2.2 方程组Ax=0和Ax=b的解 79  
2.2.1 阶梯矩阵U和行*简矩阵R 80  
2.2.2 主变量与自由变量 82  
2.2.3 求解Ax=b, Ux=c, Rx=d 84  
2.2.4 另一个实例演示 86  
习题 88  
2.3 线性无关、基和维数 94  
2.3.1 张成子空间 97  
2.3.2 向量空间的基 97  
2.3.3 向量空间的维数 99  
习题 100  
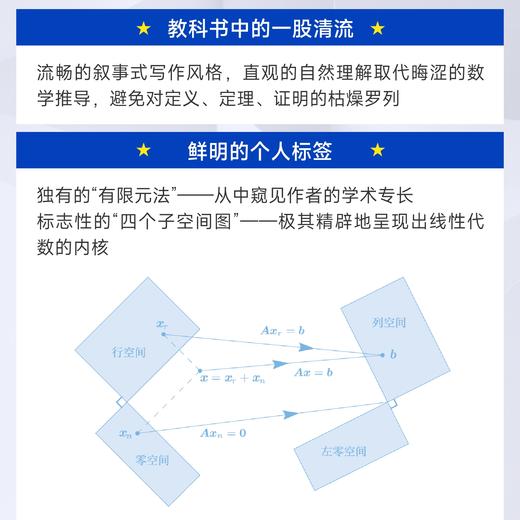
2.4 四种基本子空间 104  
2.4.1 逆的存在性 110  
2.4.2 秩为1的矩阵 112  
习题 113  
2.5 图与网络 116  
2.5.1 生成树和线性无关的行向量 119  
2.5.2 橄榄球队排名 120  
2.5.3 网络与离散应用数学 122  
习题 125  
2.6 线性变换 127  
2.6.1 变换的矩阵表示 130  
2.6.2 旋转Q、投影P、反射H 132  
习题 135  
第 2章复习题 139  
第3章 正交性 143  
3.1 正交向量与子空间 143  
3.1.1 正交向量 144  
3.1.2 正交子空间 145  
3.1.3 矩阵和子空间 148  
习题 150  
3.2 夹角余弦和直线上的投影 154  
3.2.1 内积和夹角余弦 155  
3.2.2 直线上的投影 156  
3.2.3 秩为1的投影矩阵 158  
3.2.4 内积的转置 159  
习题 160  
3.3 投影与*小二乘法 162  
3.3.1 多变量的*小二乘问题 163  
3.3.2 向量积矩阵A^{T}A 165  
3.3.3 投影矩阵 166  
3.3.4 数据的*小二乘拟合 167  
3.3.5 加权*小二乘法 170  
习题 172  
3.4 正交基与格拉姆–施密特正交化 175  
3.4.1 正交矩阵 176  
3.4.2 具有标准正交列的矩形矩阵 178  
3.4.3 格拉姆–施密特正交化过程 180  
3.4.4 QR分解 183  
3.4.5 函数空间和傅里叶级数 184  
习题 187  
3.5 快速傅里叶变换 190  
3.5.1 复数单位根 191  
3.5.2 傅里叶矩阵及其逆矩阵 193  
3.5.3 快速傅里叶变换概述 195  
3.5.4 快速傅里叶变换的完整过程和蝶形运算 197  
习题 198  
第3章复习题 199  
第4章 行列式 202  
4.1 引言 202  
4.2 行列式的性质 204  
习题 208  
4.3 行列式的公式 211  
习题 216  
4.4 行列式的应用 221  
习题 227  
第4章复习题 231  
第5章 特征值与特征向量 233  
5.1 引言 233  
5.1.1 Ax=λx的解 235  
5.1.2 小结和例题 237  
5.1.3 MATLAB中的eigshow命令 240  
习题 241  
5.2 矩阵的对角化 244  
5.2.1 对角化的例题 247  
5.2.2 幂和乘积：Ak和AB 248  
习题 250  
5.3 差分方程与矩阵的幂Ak 253  
5.3.1 斐波那契数 254  
5.3.2 马尔可夫矩阵 257  
5.3.3 u_{k+1}=Au_{k}的稳定性 259  
5.3.4 正矩阵及其在经济学中的应用 260  
习题 263  
5.4 微分方程和e^{At} 266  
5.4.1 微分方程的稳定性 270  
5.4.2 二阶方程 274  
习题 276  
5.5 复矩阵 281  
5.5.1 复数及其共轭 281  
5.5.2 复向量的长度和转置 283  
5.5.3 埃尔米特矩阵 284  
5.5.4 酉矩阵 287  
习题 290  
5.6 相似变换 293  
5.6.1 基变换=相似变换 295  
5.6.2 利用酉矩阵生成的三角形式 296  
5.6.3 对称矩阵和埃尔米特矩阵的对角化 298  
5.6.4 若尔当标准形 300  
习题 303  
特征值和特征向量的性质 307  
第5章复习题 308  
第6章 正定矩阵 311  
6.1 极小值、极大值和鞍点 311  
6.1.1 正定矩阵与不定矩阵：碗形与鞍形 312  
6.1.2 高维的情形：线性代数 314  
习题 316  
6.2 正定性的判别法 317  
6.2.1 正定矩阵与*小二乘法 320  
6.2.2 半定矩阵 321  
6.2.3 n维空间中的椭球面 322  
6.2.4 惯性定律 324  
6.2.5 广义特征值问题 326  
习题 327  
6.3 奇异值分解 331  
习题 338  
6.4 *小值原理 340  
6.4.1 条件*小值 341  
6.4.2 再说*小二乘法 343  
6.4.3 瑞利商 343  
6.4.4 特征值的缠结 344  
习题 346  
6.5 有限元法 347  
6.5.1 试验函数 348  
6.5.2 线性有限元 349  
6.5.3 特征值问题 351  
习题 351  
第7章 矩阵的计算 353  
7.1 引言 353  
7.2 矩阵的范数和条件数 354  
7.2.1 非对称矩阵 356  
7.2.2 范数公式 358  
习题 359  
7.3 特征值的计算 361  
7.3.1 三对角矩阵和海森伯格形式 363  
7.3.2 计算特征值的QR算法 366  
习题 368  
7.4 解Ax=b的迭代法 369  
习题 375  
第8章 线性规划与博弈论 378  
8.1 线性不等式 378  
8.1.1 可行集与成本函数 379  
8.1.2 松弛变量 380  
8.1.3 餐食问题及其对偶问题 381  
8.1.4 典型应用 381  
习题 382  
8.2 单纯形法 383  
8.2.1 几何方法：沿边移动 384  
8.2.2 单纯形算法 385  
8.2.3 单纯形表 387  
8.2.4 组织单纯形法的步骤 390  
8.2.5 卡马卡方法 392  
习题 393  
8.3 对偶问题 394  
8.3.1 对偶性的证明 397  
8.3.2 影子价格 398  
8.3.3 内点法 400  
8.3.4 不等式理论 401  
习题 403  
8.4 网络模型 404  
8.4.1 婚配问题 406  
8.4.2 生成树和贪婪算法 408  
8.4.3 再论网络模型 409  
习题 410  
8.5 博弈论 411  
8.5.1 矩阵博弈 413  
8.5.2 *小*定理 414  
8.5.3 实际的博弈 416  
习题 417  
附录A 空间的交、和与积 419  
附录B 若尔当标准形 426  
部分习题的答案 433  
矩阵分解 475  
词汇表 477  
MATLAB教学代码 485  
人名索引 487  
术语索引 490  
线性代数概要 500